Альтернативная версия
В 1902 г. Бернштейн выдвинул модель-гипотезу о применимости термодинамически равновесного описания потенциалов на мембране нервных волокон. Он исходил из принципа естественного равновесия между электрическим потенциалом на мембране и осмотическим давлением внутри клетки. Подкреплялась его гипотеза уравнением Нернста, позволявшем предсказать максимальный рабочий потенциал, который может быть получен в результате электрохимического взаимодействия, при известных давлении и температуре.
Эта гипотеза господствовала до 1939 года. На смену ей пришла модель Ходжкина – Хаксли, основанная на понятии об ионных каналах.
Между тем, согласно принципу Ле Шателье – Брауна: если на систему, находящуюся в устойчивом равновесии, воздействовать извне, изменяя какое-либо из условий равновесия (температура, давление, концентрация, внешнее электромагнитное поле), то в системе усиливаются процессы, направленные на компенсацию внешнего воздействия. Принцип применим к равновесию любой природы: механическому, тепловому, химическому, электрическому.
Предлагаю восстановить справедливость и рассмотреть процесс возникновения и распространения нервного импульса с учётом всех трёх составляющих (электрический потенциал, концентрация ионов и давление).
В соответствии с теорией газовой динамики граница волны повышенного давления в трубе распространяется со скоростью звука в соответствующей среде. Помните про пульсовую волну? Она тоже должна распространяться со скоростью звука в жидкости. Как объяснить сравнительно медленное фактическое распространение пульсовой волны (5–10 м/с)? Считается, что её скорость снижается благодаря упругости и эластичности кровеносных сосудов. Это хорошее объяснение, оно подводит нас к теории нелинейных волн – солитонов. Но сегодня медицина довольствуется, линейными уравнениями.
Теория скорости передачи импульса по кругу кровообращения восходит к работам Томаса Янга в 1808 году. Связь между скоростью пульсовой волны (С) и жёсткостью артериальной стенки может быть получена из второго закона движения Ньютона (F = m a) применённого к небольшому жидкостному элементу, где сила, действующая на элемент, равна произведению плотности (масса на единицу объёма - ρ) на ускорение. На практике, подход к вычислению скорости пульсовой волны аналогичен вычислению скорости звука, C0, в сжимаемой жидкости:
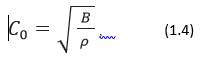
где: B - объёмный модуль, а ρ - это плотность жидкости.
Уравнение Фрэнка / Брэмуелла - Хилла
Для несжимаемой жидкости (крови) в сжимаемой (эластичной) трубке (например, артерии) Отто Фран, Джон Крайтон Брэмуэлл и Арчибальд Хилл предложили следующее уравнение :

где: r - радиус трубки, а D - растяжимость.
Формула Моенса - Кортевега
Но сегодня медицина чаще пользуется линейным уравнением, которое характеризует скорость пульсовой волны с точки зрения модуля упругости стенки сосуда, толщины стенки, и его радиуса. Оно было независимо получено Адрианом Изебри Моенсом и Дидериком Кортевегом и эквивалентно уравнению Фрэнка / Брэмуелла – Хилла.
Скорость пульсовой волны в артерии определяется с помощью формулы Моенса-Кортевега:
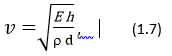
где Е – модуль упругости (модуль Юнга); ρ – плотность вещества сосуда; h – толщина стенки сосуда; d – диаметр сосуда.
Формула Моенса-Кортевега экспериментально проверена для больших сосудов (аорты, артерий и артериол).
Однако, внимательный читатель заметит, что если верить этой формуле, то скорость волны тем выше чем тоньше сосуд. На практике же все совсем наоборот.
Доказано, что при распространении нервного импульса в аксоне имеют место поверхностные механические волны, распространяющиеся совместно с электрическим потенциалом действия. Потенциал действия в гигантских аксонах кальмара сопровождается быстрым и небольшим «набуханием» и смещением поверхности около 0,5 нм, при увеличении давления на примерно 1 дин/см2. (По другим данным амплитуда изменения давления составляет около 1 мПа.)

Рисунок 59 Расширение стенок нейрона
С учётом формул Ходжкина-Хаксли (1.1), Моенса-Кортевега (1.7), и формулы Рассела (2.1), можно предложить для определения скорости нервного импульса следующую зависимость:

Где:
Е – модуль Юнга (плотность вещества), µ – коэффициент Пуассона, – модуль упругости, h – величина «набухания» клеточной мембраны, r – радиус аксона.
Е – плотность вещества мембраны нервной клетки, = 18,5*106 Па, [63]
µ – коэффициент Пуассона (0,45, за неимением лучшего взято среднее между каучуком и полиэтиленом),
ρ – модуль упругости – 800 кг/м3 (значение для мембраны, 1050 – для миелинового покрытия),
а – величина набухания клеточной мембраны, (0,5 нм, можно полагать, что a<<d)
d – диаметр нервного волокна – (100-1000 мкм для немиелинизированного и 1-20 мкм для миелинизированного волокна).
Под действием растягивающей (или сжимающей) силы изменяются не только продольные, но и поперечные размеры мембраны. Если сила ¬ растягивающая, то поперечные размеры – уменьшаются. Для учёта этого фактора вводится коэффициент Пуассона. Он зависит только от материала рассматриваемого тела. Модуль Юнга и коэффициент Пуассона полностью характеризуют упругие свойства изотропного материала.
В отличие от формулы Моенса-Кортевега здесь не учитывается толщина мембраны, она примерно одинакова для всех клеток. И второе – исправлена зависимость от диаметра волокна на обратную.
Формула 2.1 прекрасно подходит ля описания немиелинизированного нервного волокна.
Доказано. Проводимость нервов новорождённого ребёнка ниже, чем у взрослого в два раза и скорость проведения возбуждения составляет около 50% от таковой у взрослых. Проведение возбуждения по нервным волокнам «плохо изолировано».
В процессе взросления организма нервные волокна миелинизируются. Это приводит к тому, что скорость распространения потенциала действия растёт. У детей она возрастает до показателей взрослого человека к 5–9 годам для разных типов нервных тканей.
Миелинизацию можно рассматривать как «армирование» нервного волокна, которое приводит к увеличению модуля упругости мембраны – Е и, следовательно, к увеличению скорости нервного импульса.
Попробуем учесть этот фактор путём введения специального коэффициента. В простейшем случае можно использовать в качестве такового отношение длины участка, покрытого миелином – L, и длины перехвата Ранвье – l.
K= (L+l)/ l (2.3)
L – по данным разных источников расстояние между перехватами Ранвье 0,2 – 2,5 мм.
l – длина перехвата Ранвье 1-2 мкм.
В большинстве случаев, для миелинизированного волокна этот коэффициент близок к 1.
Но главное – требуется подстановка другого значения модуля Юнга (большего на значение этого показателя для миелина, покрывающего клетку) - Em.
В результате конечная формула для определения скорости нервного импульса будет выглядеть так:
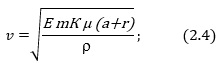
Расчёты показали удовлетворительное соответствие с экспериментальными данными для: 1) немиелинизированных нейронов и 2) миелинизированных нейронов с малыми диаметрами. А вот для миелинизированных волокон большого диаметра выявились значительные отклонения от экспериментальных (в сторону уменьшения скорости).
И это не удивительно, полученная формула применима для линейных процессов. В случае же рассмотрения процесса как солитона или ударной волны следовало бы учесть нелинейную зависимость её скорости от длительности и амплитуды (вспомним пример цунами).
Примечание. Почему не учитывается соотношение миелинизированных и немиелинизированных участков аксона сторонниками сальтаторного проведения? Вероятно, потому, что пришлось бы объяснить: почему скорость возрастает примерно на один порядок, а не на четыре. Ведь отношение длин шванновской клетки и перехвата Ранвье составляет примерно 20 000.
PS. Ложка дёгтя. Через модуль Юнга вычисляют скорость звука в веществах по формуле:
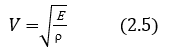
Получается я всего лишь определил скорость звука в мембране с поправками, коэффициентами и эмпирически увязанный с диаметром аксона?
Да, но формула (2.5) используется и для определения скорости ударной волны при условии, что модуль упругости стенки трубы стремится к бесконечности. А в нашем случае обязательно нужно учесть упругое расширение стенки мембраны!
Такая формула существует и успешно применяется в гидродинамике для исследования ударных волн:
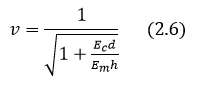
- Ес – модуль упругости сомы,
- d – диаметр аксона,
- Еm – модуль упругости мембраны,
- h – толщина мембраны.
Что ж, значит уравнение скорости нервного импульса продолжает оставаться тайной. И возможно ещё ждёт своего нобелевского лауреата.
Зачем нужна формула скорости нервного импульса? Разве недостаточно экспериментальных измерений? На мой взгляд важна не сама формула, а объяснение физического смысла процесса и его математического описания. А в формуле Θ = 6 d его, увы, нет. И если принять за основу правильность всего математического аппарата созданного наукой, то приходится сомневаться в правильности современной трактовки физических процессов при распространении нервного импульса.
Статья по теме Скорость нервного импульса (pdf)
- Скорость нервного импульса (Гкпман Гельмгольц)
- Реотом Бернштейна
- Скорость нервного импульса. Миелин
- Определение скорости нервного импульса через ионную теорию