Солитон
Большинству людей, безусловно, знакомы такие слова как электрон, протон, нейтрон, фотон. А вот созвучное им слово – солитон, возможно, знакомо не многим. Это и неудивительно: хотя явление, обозначаемое этим словом, известно без малого два столетия, должное внимание солитонам стали уделять лишь с последней трети ХХ века. Что же это такое – солитон? [51]
Попробуем разобраться с солитонами, и при этом по возможности обойтись без математики. Однако, нам всё же придётся поговорить о двух явлениях, лежащих в основе механизма образования солитонов – о нелинейности и дисперсии.
Но сначала история о том, как и когда был обнаружен солитон.
...Это случилось в 1834 году. Джон Скотт Рассел (John Scott Russell; 1808 — 1882) , шотландский физик и талантливый инженер-изобретатель, принял предложение оценить возможности навигации паровых судов по каналу, соединяющему Эдинбург и Глазго. В то время перевозки по каналу осуществлялись с помощью небольших барж на конной тяге. Предстояло выяснить, как переоборудовать баржи при переходе с конной тяги на паровую. Рассел вёл наблюдения за разнообразными баржами, движущимися с разными скоростями. И во время этих наблюдений он столкнулся с очень странным явлением.
Вот как он описал его в своём Докладе о волнах: «Я следил за движением баржи, которую быстро тянула по узкому каналу пара лошадей, когда баржа неожиданно остановилась. Но масса воды, которую баржа привела в движение, собралась около носа судна в состоянии бешеного движения, затем неожиданно оставила его позади, катясь вперёд с огромной скоростью и принимая форму большого одиночного возвышения – округлого, гладкого и чётко выраженного водяного холма. Он продолжал свой путь вдоль канала, нисколько не меняя своей формы и не снижая скорости. Я последовал за ним верхо́м, и когда нагнал его, он по-прежнему катился вперёд со скоростью примерно 8–9 миль в час, сохранив свой первоначальный профиль возвышения длиной около тридцати футов и высотой от фута до полутора футов. Его высота постепенно уменьшалась, и после одной или двух миль погони я потерял его в изгибах канала». [52]
Рассел назвал обнаруженное им явление «уединённой волной трансляции». Однако его сообщение было встречено с недоверием, признанные корифеи в области гидродинамики – Джордж Биддель Эйри (George Biddell Airy; 1801—1892) и Джордж Габрие́ль Стокс (Stokes, George Gabriel; 1819–1903), утверждали на основании общепринятых в то время уравнений гидромеханики, что волны при распространении на значительные расстояния не могут сохранять свою форму.
Признание уединённой волны случилось ещё при жизни Рассела трудами нескольких математиков, которые доказали, что существовать она может, а, кроме того, были повторены и подтверждены опыты самого Рассела. Но дискуссии по поводу солитона ещё долго не прекращались – слишком велик был авторитет Эйри и Стокса.
Позже, учёные следующего поколения Жозеф Валентин де Буссинеск и его сверстник лорд Рэлей сумели найти приближённое математическое описание формы и скорости уединённой волны на мелкой воде. Вскоре появились ещё две – три математические работы об уединённой волне, а также вновь были повторены и подтверждены опыты Рассела.
Итоговую черту под спором подвели голландские математики Дидерик Иоханнес Кортевег (Diederik Johannes Korteweg, 1848 – 1941) и его ученик Густав де Фриз (Gustav de Vries, 1866 – 1934). В 1895 году, спустя тринадцать лет после смерти Рассела, они нашли точное уравнение, волновые решения которого полностью описывало происходящие процессы. В первом приближении это можно пояснить следующим образом. Волны Кортевега – де Фриза имеют несинусоидальную форму и становятся синусоидальными только в том случае, когда их амплитуда очень мала. При увеличении длины волны вершины синусоиды приобретают вид далеко разнесённых друг от друга горбов, а при очень большой длине волны остаётся один горбик, который и соответствует «уединённой» волне. Уравнение Кортевега – де Фриза (КдФ-уравнение) было по-настоящему оценено уже в наши дни, когда физики поняли его универсальность и возможность применения к волнам различной природы. Самое главное то, что оно описывает процесс распространения нелинейных волн, и настало время более подробно остановиться на этом понятии. [51]
В теории обычных волн фундаментальное значение имеет волновое уравнение. Не вдаваясь в высшую математику, отметим лишь, что и функция, описывающая волну, и связанные с ней переменные содержатся в нём в первой степени. Такие уравнения называются линейными. Решением волнового уравнения служит линейная гармоническая (синусоидальная) волна. То есть термин линейная употребляется здесь не в геометрическом смысле (синусоида – не прямая линия), а в смысле использования первой степени величин в волновом уравнении. [51]
Линейные волны подчиняются принципу суперпозиции (сложения). Это означает, что при наложении нескольких линейных волн результирующая волна представляет собой простую сумму исходных волн. Так происходит потому, что каждая волна распространяется в среде независимо от прочих, между ними нет ни обмена энергией, ни иного взаимодействия, они свободно проходят друг сквозь друга. В большинстве случаев это справедливо для световых, звуковых и радиоволн, и даже для волн, которые рассматриваются в квантовой теории. Но для волн в жидкости это верно только при сложении волн очень маленькой амплитуды. Дело в том, что уравнения гидродинамики нелинейны.
Напомним, скорость распространения фазы волны (так называемая фазовая скорость) зависит от длины волны, это явление называется дисперсией. А любую несинусоидальную волну можно представить совокупностью простых синусоидальных составляющих с различными частотами (длинами волн), амплитудами и начальными фазами (по теореме Фурье). Из-за дисперсии эти составляющие распространяются с различными фазовыми скоростями, что приводит к разрушению формы волны при её распространении. Но солитон, который тоже можно представить, как сумму указанных составляющих при движении свою форму сохраняет. Почему? Вспомним, что солитон – волна нелинейная. В этом-то и кроется его загадка. Дело в том, что солитон рождается в тот момент, когда эффект нелинейности, делающий гребень солитона более крутым и стремящийся его опрокинуть, компенсируется влиянием дисперсии, стремящейся его размыть и делающей его более пологим. Таким образом солитон возникает на стыке нелинейности и дисперсии, уравновешивающих друг друга. Попробуем рассмотреть это явление на примере цунами.
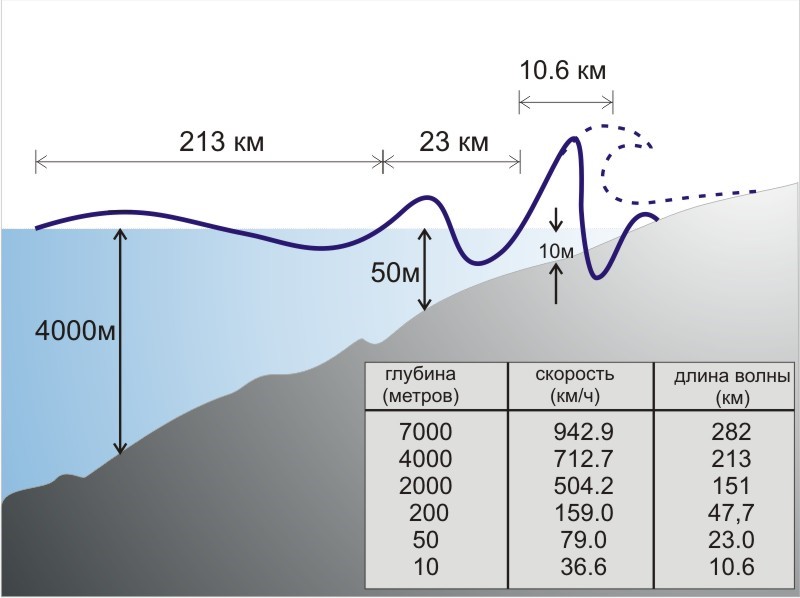
Цунами (в переводе с японского – широкая/длинная волна) – это длинные волны, возникающие в океане в следствии подводных землетрясений, приводящих к резким вертикальным смещениям морского дна. В момент такого смещения, направленного вверх, над эпицентром землетрясения возникает волна высотой до пяти метров.
В открытом океане волны цунами распространяются со скоростью:

где g – ускорение свободного падения, а h – глубина океана. При средней глубине 4000 метров скорость распространения составляет 200 м/с (720 км/час). В открытом океане высота волны редко бывает больше одного метра, при этом длина волны (расстояние между гребнями) может быть 500–1000 километров, такая волна не опасна для судоходства.
Зато при выходе волны на мелководье, происходит удивительное явление: её скорость и длина уменьшаются, а высота увеличивается. В результате у берега её высота может достигать до 30–40 метров. Цунами обычно проявляется как серия волн, но так как волны длинные, то между приходами волн может проходить более часа.
При формировании гигантского вала цунами происходит втягивание в него огромных масс воды что приводит к постепенному отступлению воды от берега на значительное расстояние и обнажение дна. Чем дальше отступает океан, тем выше будет волна цунами.
В 1965 г. американские учёные М. Крускал и Н. Забуски, изучая явления столкновений уединённых волн с помощью моделирования на ЭВМ, заметили, что уединённые волны во многом подобны частицам, они немедленно убрали слово «волна», а из «уединённой» (solitary) составили термин «солитон» (soliton). Первоначально солитон был назван «солитроном», по созвучию с другой элементарной частицей – электроном. Однако в последний момент стало известно о существовании некоей фирмы «Солитрон», и авторам пришлось убрать «р», чтобы не вступать в противоречие с законодательством о защите авторских прав. Фирма давно канула в Лету, а солитон живёт и здравствует! [51]
Уже в наше время были открыты наиболее удивительные свойства солитонов, благодаря которым они стали предметом перспективных научных поисков. Одно из уникальных свойств уединённых волн состоит в том, что они во многом похожи на частицы. Например, при столкновении два солитона не проходят сквозь друг друга, подобно обычным линейным волнам, а как бы отталкиваются друг от друга подобно бильярдным шарам.
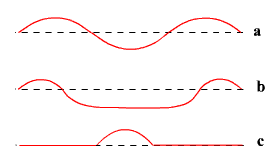
Обычная линейная волна имеет форму правильной синусоиды (а). Нелинейная волна Кортевега – де Фриза на графике представляет собой последовательность далеко разнесённых горбиков, разделённых слабовыраженной впадиной (b). При очень большой длине волны от неё остаётся только один горб – «уединённая волна», или солитон (c).
Как ведёт себя нелинейная волна на поверхности воды при отсутствии дисперсии? Её скорость не зависит от длины волны, но возрастает с увеличением амплитуды. Вершина волны движется быстрее, чем её подошва, фронт становится всё круче и, наконец, волна опрокидывается. Но одиночную волну на воде можно представить в виде совокупности простых синусоидальных составляющих отличающихся длиной волны. В среде обладающей дисперсией, длинные волны побегут быстрее коротких, размывая крутизну фронта. При определённых условиях дисперсия полностью компенсирует влияние нелинейности, наступит равновесие, и волна будет долго сохранять свою форму – так рождается солитон.
На поверхности воды могут формироваться и групповые солитоны. В реальности именно они, а не бесконечные синусоидальные волны наблюдаются на поверхности моря. Групповой солитон чем-то напоминает амплитудно-модулированные электромагнитные волны; его огибающая несинусоидальна, она описывается более сложной функцией – гиперболическим секансом. В отличии от КдФ-солитонов скорость групповых солитонов не зависит от амплитуды. Под огибающей обычно находится не более 14–20 волн. Самая высокая – волна в группе (средняя) оказывается, в интервале от седьмой до десятой; отсюда известное наблюдение про 9-й вал.
Целенаправленное изучение солитонов началось сравнительно недавно (1960-е годы). Тем не менее возможные области практического применения этого феномена уже охватывают многие области современной техники. Наибольшую популярность получили они в оптико-волоконных системах передачи информации, принцип действия которых основан на способности оптических солитонов распространяться на большие расстояния без существенного искажения формы.
К сожалению, после того как появился соответствующий математический аппарат описания нелинейных волн, к идее Германа (см. главу Гипотезы Лудимара Германа) уже не возвращались вплоть до нынешнего XXI века.
Солитонные модели :